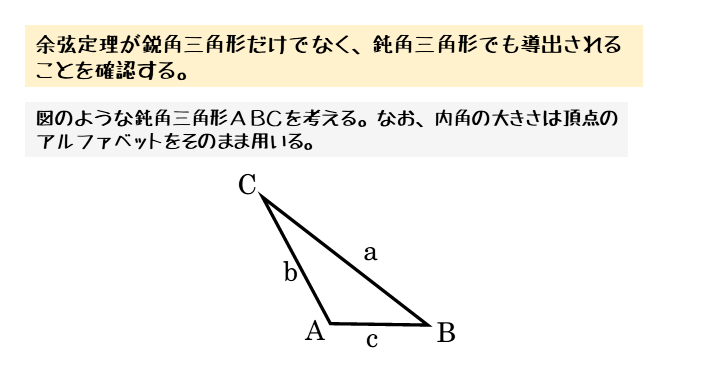
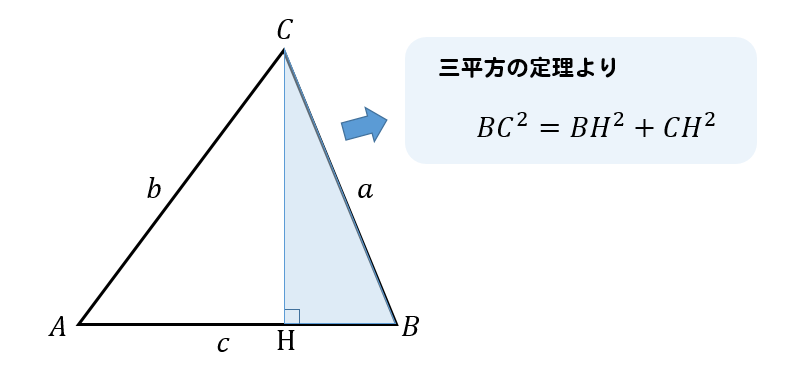
余弦定理 三 平方 の 定理 角度 310245

 余弦定理： 三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。 即： 思考3：你还有其它方法证明余弦定理吗？1、定理的内容 文字语言：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 符号语言： a2 = b2 c2 − 2bccosA b2 = c2 a2 − 2cacosB c2 = a2 b2 − 2abcosC 当 A = π 2 时，余弦定理变形为 a2 = b2 c2 ，即勾股定理，故我们说勾股・sin2θ＋cos2θ＝1を三 平方の定理として捉え ることができる。 見方や考え方 ・三角比の相互関係を利 用して,1つの値から 残りの値が求められ る。 知識理解 6 B＞90°－θの三角比 ・公式の丸覚えでは なく,図から考え られるように活 用する。

図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん

余弦定理 三 平方 の 定理 角度

余弦定理 三 平方 の 定理 角度-但是简单的同时更加要求我们的仔细严谨程度，切记不要出现忘平方、忘开根号等低级错误。 ： 余弦定理设三角形的三边为a b c,他们的对角分别为A B C,则称关系式 a^2=b^2 c^22bc*cosA b^2=c^2 a^22ac*cosB c^2=a^2 b^22ab*cosC 正弦定理 三角函数角度对照表;求角度的简易形式 上面我们看到已知三边是怎样去求角度。我们用了几步来做，但其实用 "直接" 公式会比较简单（公式只不过是重排这公式： c 2 = a 2 b 2 − 2ab cos ）。公式可以有三个形式： cos = a 2 b 2 − c 2 2ab cos(A) = b 2 c 2 − a 2 2bc cos(B) = c 2 a 2 − b

正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

中線定理の証明の方針 教科書にも載っている中線定理ですが，正弦定理や余弦定理などの花型公式と比べるとやや地味な感じがします。 しかし，中線定理は様々な手法で証明できるので， 図形の証明問題のよい題材です。 このページでは中線定理の証明 余弦定理 三角形任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的积的两倍。 即在三角形ABC中,已知AB=c,BC=a,CA=b,则有： a2=b2c22bccosA b2=a2c22accosB c2=a2b22abcosC 展开全文 余弦定理平面几何证法 在任意 ABC中，做AD⊥BC毕氏定理（英语： Pythagorean theorem / Pythagoras' theorem）是平面几何中一个基本而重要的定理。 毕氏定理说明，平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方。 反之，若平面上三角形中两边长的平方和等于第三边边长的平方，则它是直角三

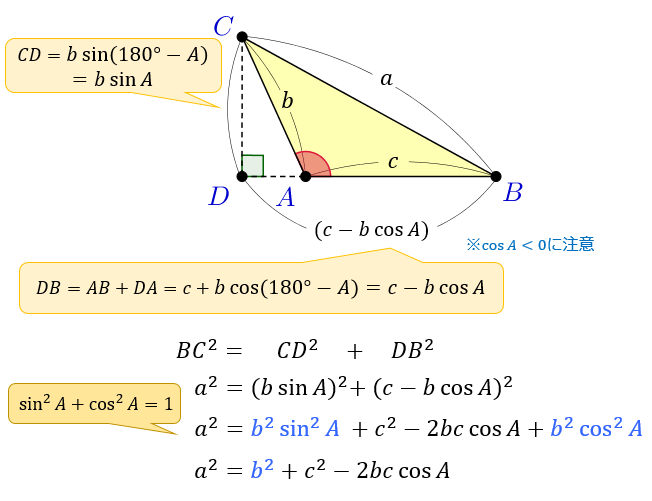
正弦、余弦和正切 三角法里的三个主要函数是 正弦 以给定角度 θ，这三 勾股定理说：在直角三角形里，a的平方加b的平方等于c已知三棱锥底面是边长为1的正三角形，侧棱长均为2，则侧棱与底面所成角的余弦值为（ ） 1年前 1个回答 已知三角形的三个角的度数,且已知其中一条边的边长,求这个三角形的面积及其他两条边的边长これが，余弦定理である．この定理は，二辺（b,c）とその間の角（∠A）が決まれば，他の辺（a） の長さが求まることを意味する．また式を変形し，cosA = b 2c2−a2 2bc とすれば，三辺の長さから角度 が求まることを意味する．

 余弦定理导学案 1 部分包含数学公式或PPT动画的文件，查看预览时可能会显示错乱或异常，文件下载后无此问题，请放心下载。 2 本文档有教师用户上传，莲山课件网负责整理代发布。 如果您对本文档有争议请及时联系客服。 3 部分文档可能由于网络波动ピタゴラスの定理（ピタゴラスのていり）は、直角三角形の3辺の長さの関係を表す等式である。三平方の定理（さんへいほうのていり）、勾股弦の定理（こうこげんのていり）とも呼ばれる。1 1 概要 2 ピタゴラス数 21 ピタゴラス数の性質 22 Jesmanowicz 予想 3 一般化 31 角の一般化 32 指数の この式で を代入すると、 なので、三平方の定理の形になり、余弦定理は三平方の定理において角度を一般化したものと考えられます。 このあたりまでは学校や塾で話されることが多いのですが、では次元と角度を一遍に一般化したらどうなるでしょうか。

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

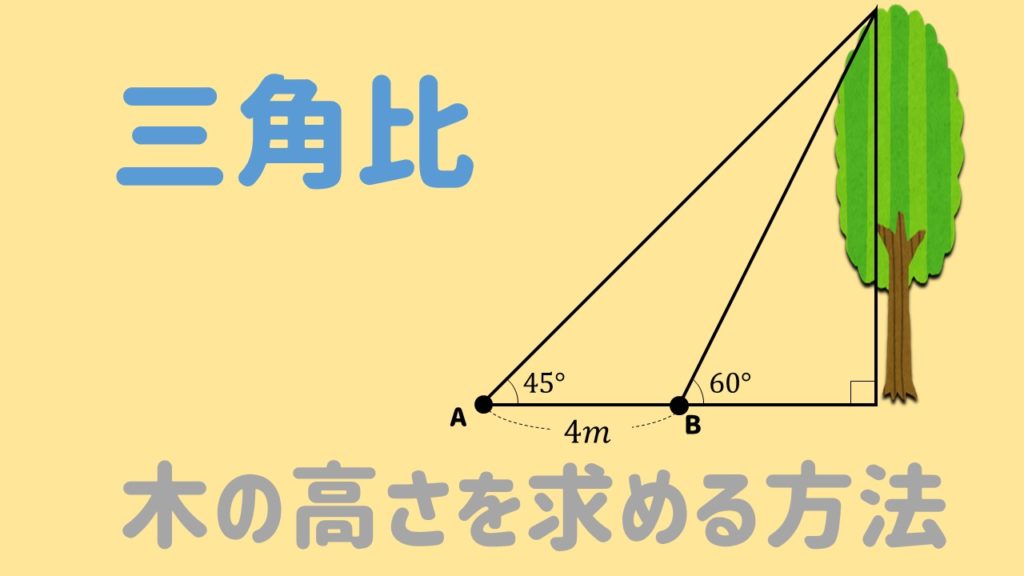
高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

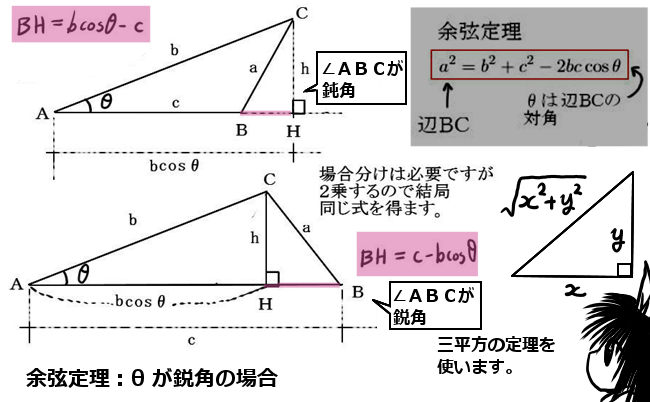
三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます： a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 （正確には、角 A そのものではなく cos A が求まりますが正余弦定理性质 对于任意三角形，任何一边的 平方 等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，若三边为a，b，c 三角为A，B，C ，则满足性质—— S ABC=1/2absinC S ABC=1/2bcsinA S ABC=1/2acsinB （ 物理力学 方面的 平行四边形定则 中也会用到） 第一余弦定理 （ 任意三角形 射影定理 ） 设 ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有 a=b·cos Cc·cos B

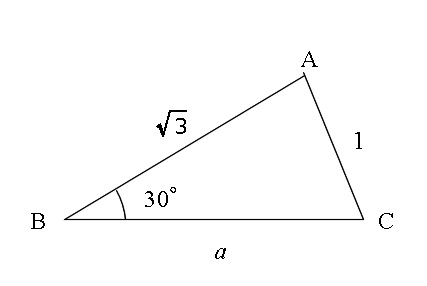
正弦定理と余弦定理を使い分ける問題の見分け方

図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん

4、将三角形的解还原为实际问题，注意实际问题中的单位、近似计算要求 典型例题2 三、解三角形应用题常有以下两种情形 1、实际问题经抽象概括后，已知量与未知量全部集中在一个三角形中，可用正弦定理或余弦定理求解 ですから， 余弦定理の場合は − 2 b c cos ⁡ θ の項が三平方の定理に付け加えられているだけですね． つまり， ∠ A が 90 ∘ から θ に変わると，三平方の定理の等式が − 2 b c cos ⁡ θ 分だけズレるということになっているわけです． このように見る 勾股定理指出直角三角形两直角边 (即"勾"、"股")边长平方和等于斜边 (即"弦")边长的平方 也就是说, 勾股定理是余弦定理在直角三角形中的应用 余弦定理适用于所有的三角形中,而勾股定理只是用于直角三角形 当余弦定理中角C等于90度时,cosC=0,就变成了勾股定理 为什么我用勾股定理和三角函数得出得答案不一样 ： 勾股定理你已经写了三角函数∠B=60°AD=AB

余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

余弦定理（也叫做余弦公式）是托勒密定理的推广 ： = 也可表示为： = 余弦定理用于在一个三角形的两个边和一个角已知时确定未知的数据。 正切定理三角函数锐角三角函数其他三个三角函数三角函数在四个象限中的符号特殊三角函数值三角形中的有关公式内角和定理正弦定理余弦定理 平方关系 $\sin^2(\alpha)\cos^2(\alpha)=1$ id 分类： 全国, 19 资源大小：1601kb 资料简介 三余弦定理（又叫最小角定理或爪子定理） （1）定理设点 为平面 上一点,过 点的斜线在平面 上的射影为 , 为平面 上的任意直线,那么 , , 三角的余弦关系为 即斜线与平面一条直线夹角 的余弦值等于斜线与平面所成角 的余弦值乘以射

勉強しよう数学解答集 余弦定理を使って角度を求める解答

図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん

 勾股定理和三角函数算出来不一样 ： 你确定?A30°,角B60°,角C90°,这个角度怎么可能AC长为4,BC长度为3?你这个角度的话三条边比例为12√￣3题都是错的 勾股定理和三角函数求的值不一样： 勾股定理在一个直角三角形中,斜边边长的平方等于两条直角边边长平方加法定理(数学 ii)のもとで, 正弦定理, 余弦定理(第一余弦定理, 第二余弦定理)は同値である(こちらとこちらを参照) この逆は, 余弦の加法定理を用いて, 次のように証明できる余弦定理（よげんていり、英 law of cosines, cosine formula ）とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。 余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別さ

21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

わかりやすい三角比と基本公式 Irohabook

思考6：勾股定理指出了直角三角形中三边平方之间的关系，余弦定理则指出了一般三角 形中三边平方之间的关系，如何看这两个定理之间的关系 （由学生总结）若ABC中，C=900，则cosC0，这时c2a2b2 由此可知余弦定理是勾股定理的推广，勾股定理是余弦定理的特例。 当已知三角形的三边，可以由余弦定理得到三角形的三个内角。 当已知三角形的三边，可以由余弦定理得到三角形的面积。 求边 余弦定理公式可变换为以下形式： 因此，如果知道了三角形的两边及其夹角，可由余弦定理得出已知角的对边。 求角 因为余弦 余弦定理(文字表述）：三角形中任何一边的平方等于其他两边的平方的和减去 这两边与它们的夹角的余弦的积的两倍．即 c =a b 2abcosC a =b c 2bccosA b =a c 2accosB

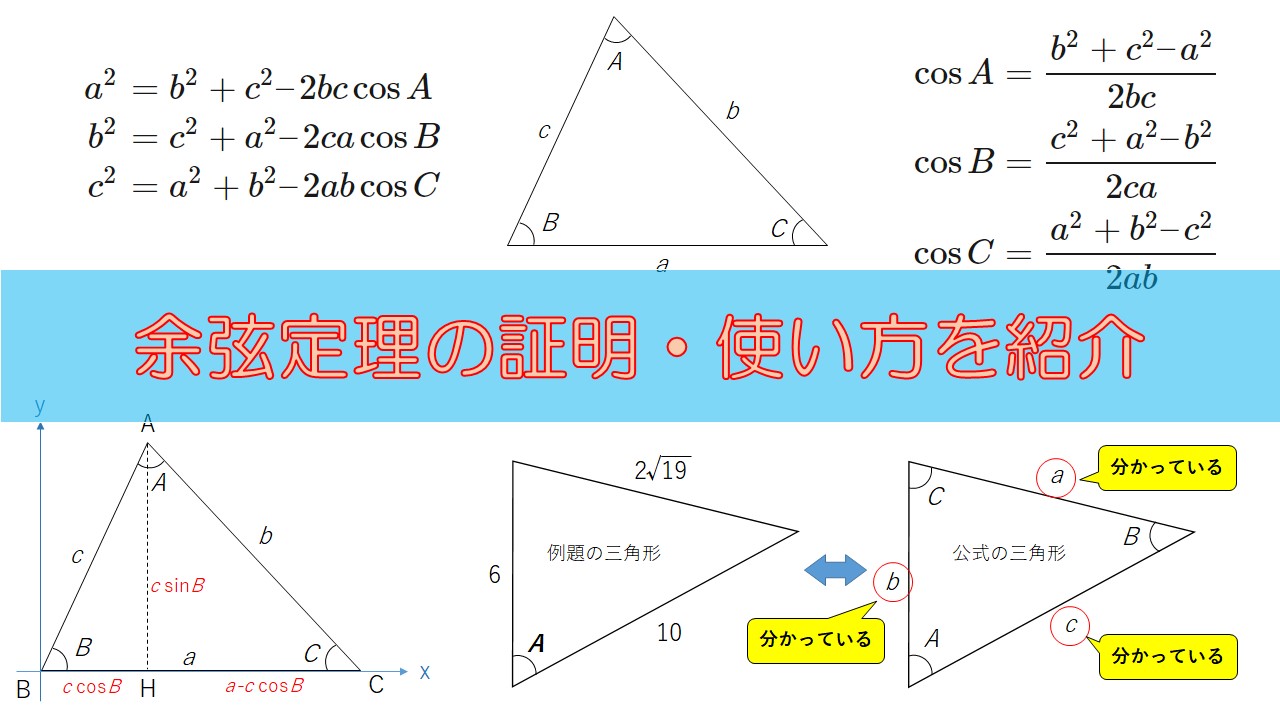
高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

５分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ

余弦定理平方求角度问题 去下载 下载需先安装客户端 客户端特权 3倍流畅播放 免费蓝光 极速下载 icon/18px/phonegrey 手机看 余弦定理平方求角度问题 当前播放至 0000 扫一扫 手机继续看 iPhone客户端 iPad客户端 Android客户端

余弦定理 Wikipedia

余弦定理の指導の細かすぎる工夫１ 怜悧玲瓏 高校数学を天空から俯瞰する

三角形の三辺がわかっているとき どこかの角度が欲しい場合 どこでもよい Yahoo 知恵袋

Http Www Infra Kochi Tech Ac Jp Takagi Survey1 6trilateration Pdf

3分で分かる 余弦定理の公式と証明 使い方のコツをわかりやすく 合格サプリ

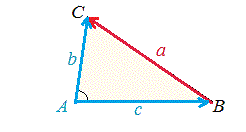
余弦定理

余弦定理 公式の証明と使い方を工学博士が解説 5分でok Rikeinvest

余弦定理の証明 簡単にわかりやすく考えてみよう 数スタ

正弦定理の公式の覚え方とは 問題の解き方や余弦定理との使い分けもわかりやすく解説 遊ぶ数学

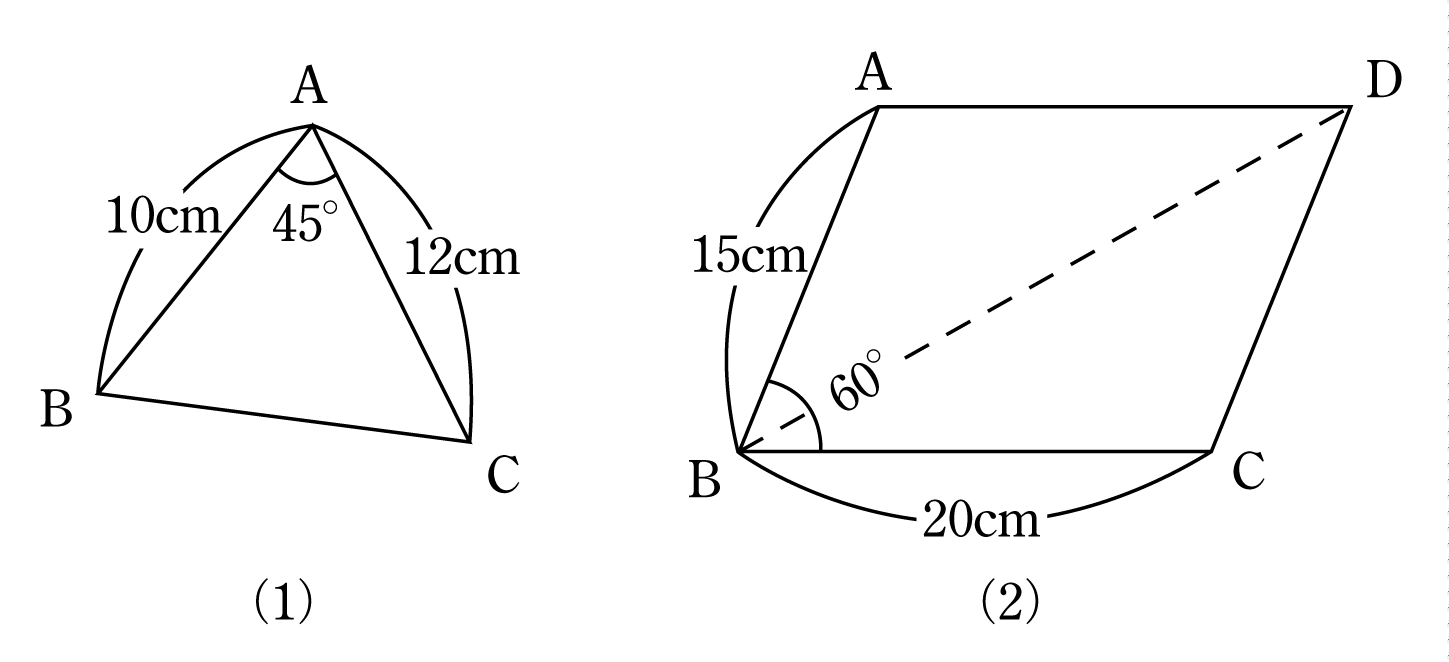
余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

補足 正弦定理と余弦定理の導出 高校数学の知識庫

三角関数 の基本的な定理とその有用性を再確認してみませんか その１ 正弦定理 余弦定理 正接定理 ニッセイ基礎研究所

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

余弦定理の証明 公式の使い方を解説 センター過去問の解説付き Studyplus スタディプラス

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

Atcoder Abc 168 C Colon 灰色 300 点 けんちょんの競プロ精進記録

５分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

余弦定理 公式の証明と使い方を工学博士が解説 5分でok Rikeinvest

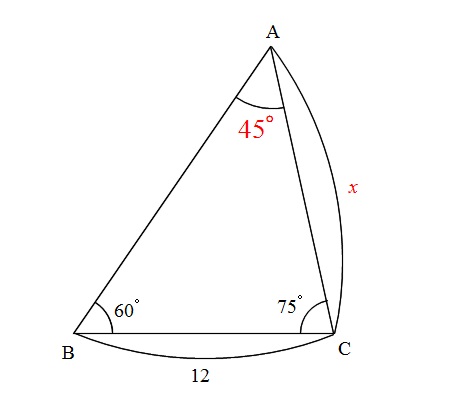
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

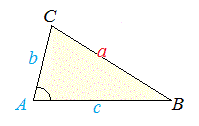
余弦定理

3

余弦定理 三平方の定理をちょろっと変えてみる キソカラ

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

余弦定理 理数系無料オンライン学習 Kori

難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門

3分で分かる 余弦定理の公式と証明 使い方のコツをわかりやすく 合格サプリ

難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門

難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門

余弦定理の覚え方 語呂合わせやイメージで暗記しよう 数学の面白いこと 役に立つことをまとめたサイト

3

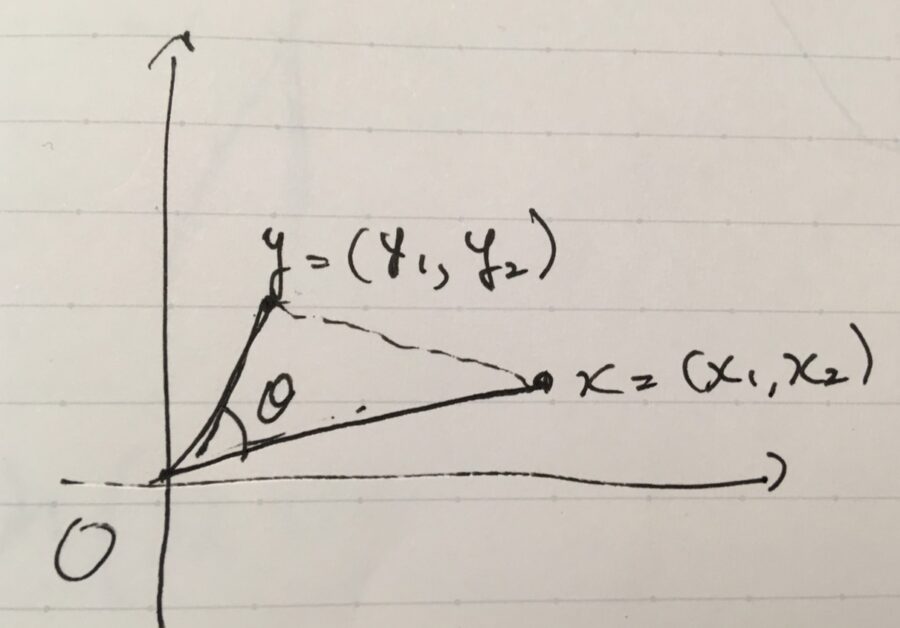
余弦定理とベクトルの内積の関係 なぜコサインか 趣味の大学数学

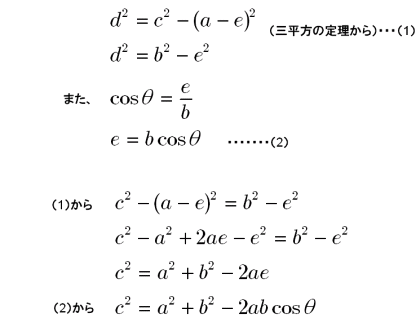
三角比 余弦定理 大人が学び直す数学

三角比 高校物理の備忘録

3分でわかる 余弦定理の公式や使い方をイラスト付きで詳しく解説

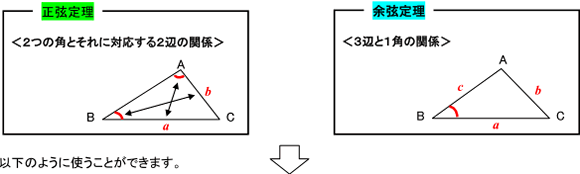
正弦定理と余弦定理のどっちを使えばいいんですか 数学 苦手解決q A 進研ゼミ高校講座

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

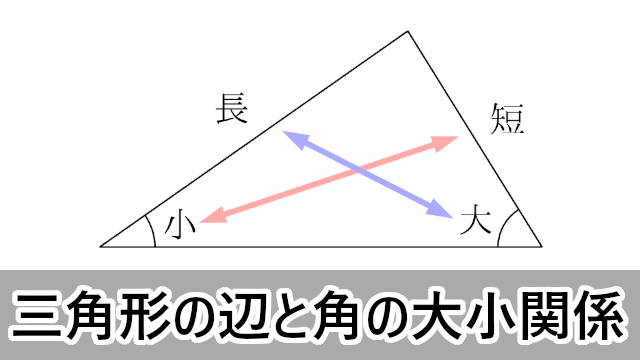
数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法

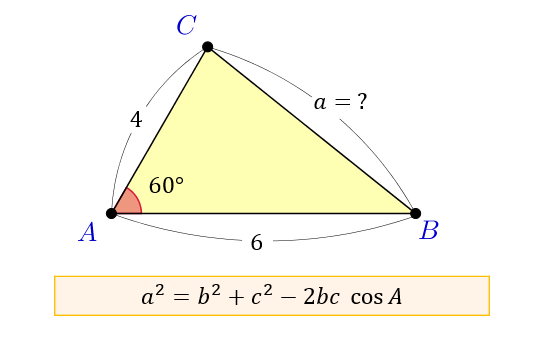
余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

勉強しよう数学解答集 余弦定理を使って角度を求める解答

余弦定理 変形 3辺から角度を求める 一夜漬け高校数学124 Youtube

職業訓練試験用対策 忘れた方 勉強方法が分からない方のためのサイン コサイン タンジェント 三角比 解説例題集 ふくなんログ

三平方の定理 自動計算サイト

余弦定理

3

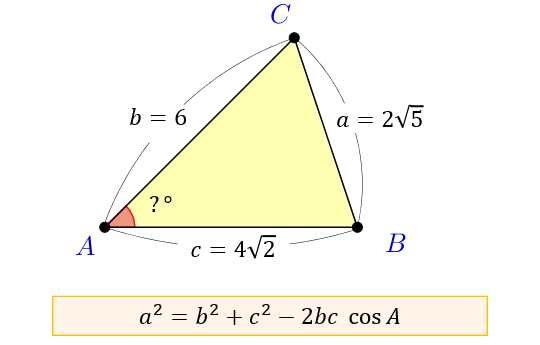
余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

数1の 1 問題です 角abhは60度ですよね Clear

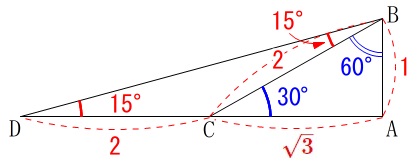
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

三角比 高校物理の備忘録

高校数学 正弦定理 比例式 と余弦定理 受験の月

3

中三です 三平方の定理の問題が分かりません 三角形の面積を求めるものです Yahoo 知恵袋

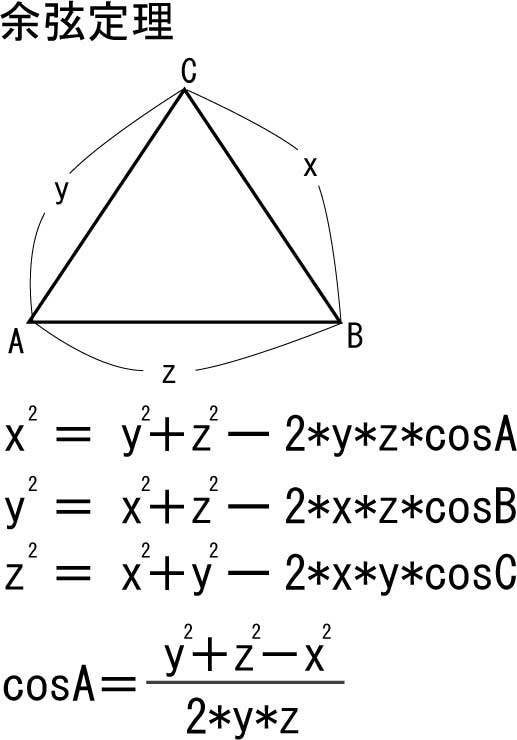
正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

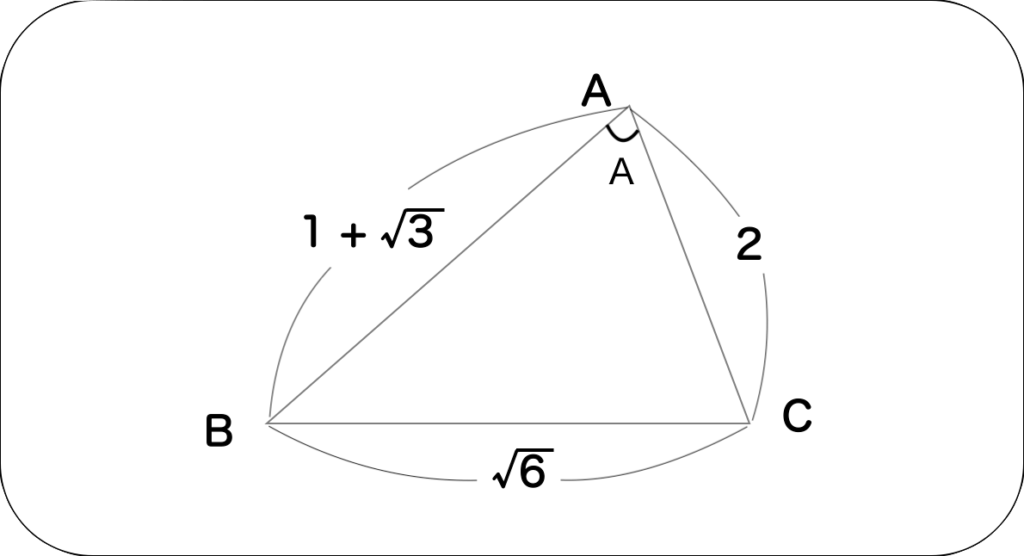
3分でわかる 余弦定理の公式や使い方をイラスト付きで詳しく解説

高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月

第１余弦定理から第２余弦定理へ 身勝手な主張

1研究中 C 数学２ 正弦定理 余弦定理 円周角の定理と外角の定理と四角形の外接円

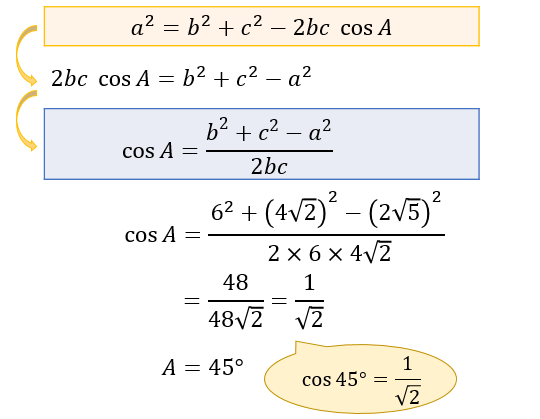
余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

三角比 高校物理の備忘録

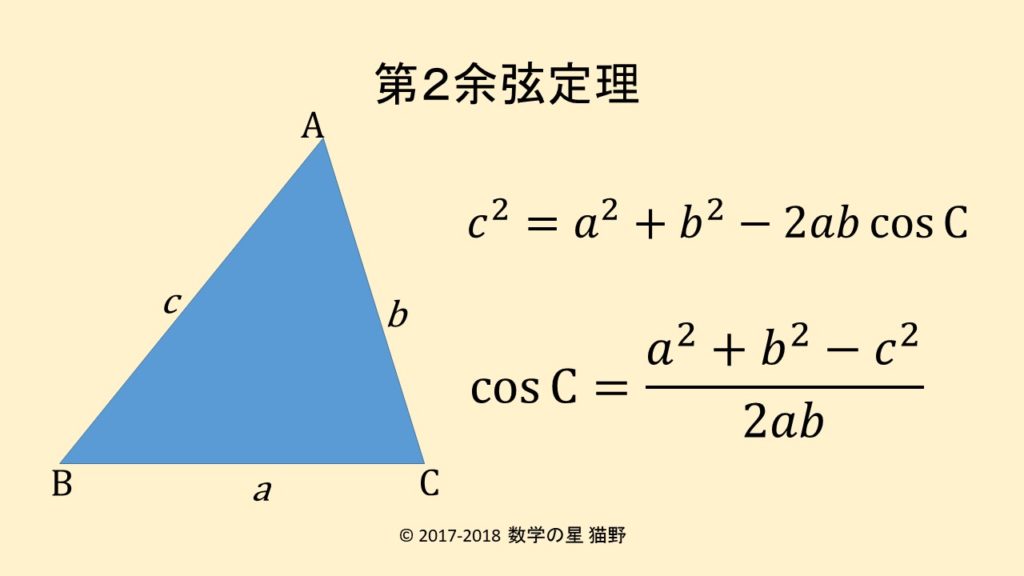
第２余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

余弦定理の公式 証明 使い方を徹底解説 例題あり 受験スタイル

余弦定理 Instagram Posts Gramho Com

高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

余弦定理 は三平方の定理の進化版 余弦定理は2つある

世界は三角関数を待っていた もうわかりましたね サー 何が いや どうすればいいかですよ サー とりあえず 速度を求めるために 目標艦の移動距離を出すんです てへ 余弦定理 余弦定理を使うんですよ

マスマスプラス Vol 59 15年秋冬号 ページ 10

数学 三角比 余弦定理の利用 残りの辺の長さを求める オンライン無料塾 ターンナップ

余弦定理 をclasspad Netで証明してみる Mathapp Days

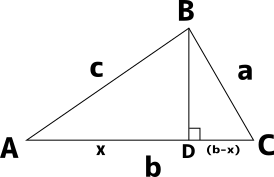
三角比を使った問題1 チーム エン

余弦定理の指導の細かすぎる工夫１ 怜悧玲瓏 高校数学を天空から俯瞰する

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

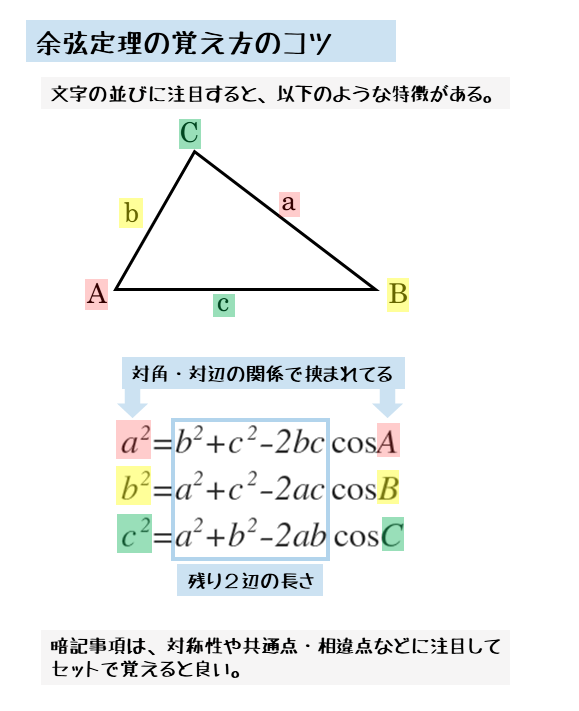
図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん

正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

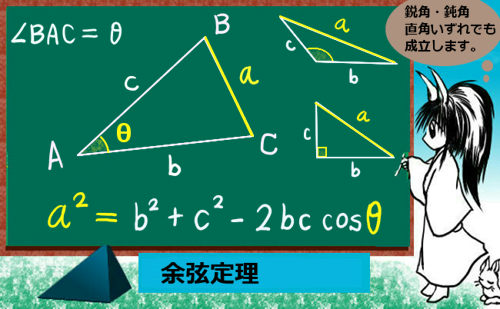
余弦定理 理数系無料オンライン学習 Kori

余弦定理で角度を求める方法 数学の星

七五三 三角形から円に内接する四角形へ

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典

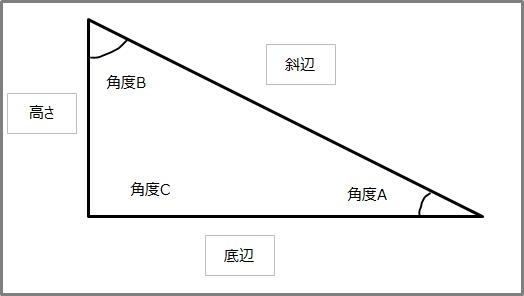
三平方の定理の計算 角度と長さ Nujonoa Blog

５分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ

余弦定理の証明 公式の使い方を解説 センター過去問の解説付き Studyplus スタディプラス

勉強しよう数学解答集 余弦定理を使って角度を求める解答

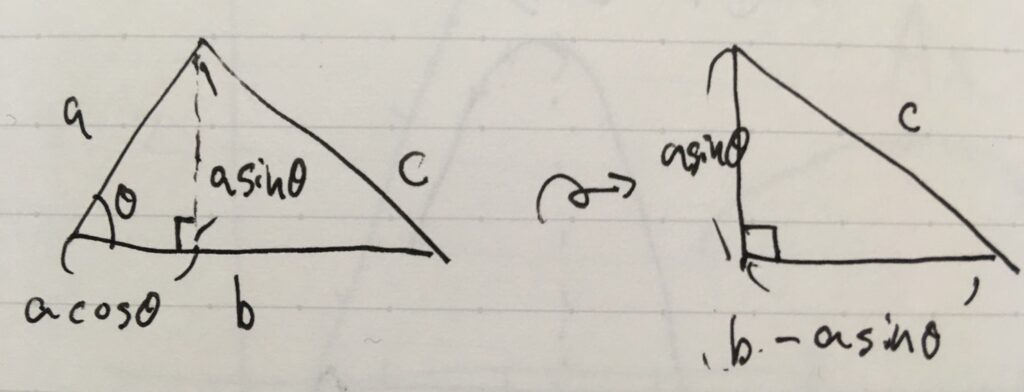
余弦定理とベクトルの内積の関係 なぜコサインか 趣味の大学数学

余弦定理の公式をマスターしよう スタディクラブ情報局

余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学

余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典

余弦定理 公式の証明と使い方を工学博士が解説 5分でok Rikeinvest

余弦定理 をclasspad Netで証明してみる Mathapp Days

余弦定理の証明 公式の使い方を解説 センター過去問の解説付き Studyplus スタディプラス

余弦定理の公式 覚え方はどうする 角度の求め方などを解説 数スタ